Research on SMART::tests
Research Goals
One of the major challenges in teaching mathematics is to provide personalised learning opportunities that meet the needs of individual students. Many students have misconceptions or gaps in their knowledge which are a barrier for further learning but often go unaddressed. SMART::tests aim to give teachers readily useable information about each student's understandings to help the teachers select instruction that will bring about specific conceptual changes.
"Specific mathematics assessments that reveal thinking", which we call SMART::tests, consist of mathematical questions that probe students' mathematical thinking and knowledge of key ideas. Many of the SMART::tests were first developed in research studies, local and international, and one of the goals of this project was to make the substantial research knowledge about students' mathematical thinking readily available in classrooms.
Research on smart tests revolved around (i) learning and (2) teaching. The learning questions were related to how students learn the individual topics that are tested in SMART::tests - what are the stages which students go through, what are the common errors and misconceptions, how can these be identified in a computer-based test, and what teaching strategies are most helpful? The teaching questions are about the use of formative assessment - how can formative assessment tools be designed for easy, practical use by teachers, what information do teachers find most useful for their teaching, and what are the outcomes for students of using this system of formative assessment.
The SMART::test project investigated two fundamental hypotheses:
- if teachers have easy access to information about their students' thinking and they make use of resources that target the development of conceptual understanding, then student achievement will increase;
- teachers' mathematics pedagogical content knowledge will increase if they have easy access to information about their students' thinking. In turn, this will further improve teaching, and hence learning.
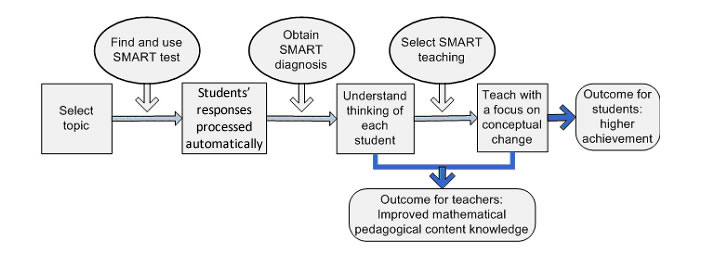 |
| Figure 1. How teachers use smart resources to bring about higher student achievement, and how this encourages teacher growth. |
The first research phase was named "Supporting personalised learning in
secondary schools through the use of specific mathematics assessments that reveal
thinking". This project was conducted at the University of Melbourne by
Professor Kaye Stacey, Dr Helen Chick and Dr Vicki Steinle. It was funded by
the Australian Research Council Linkage Projects Program LP0882176 in
partnership with the Department of Education and Early Childhood Development,
Victoria (2008 - 2010). The project officers were Ms Beth Price and Dr Eugene
Gvozdenko. Later research has been funded from a variety of sources.

SMART::tests is an expert system for teaching
There is a substantial body of research into students' mathematical thinking that has been accumulated internationally, and to which we have contributed ourselves (Stacey: number, algebra, working mathematically; Steinle: number; Chick: chance and data). However, such research needs considerable transformation for maximum effectiveness for teaching. One example of research that was ready to use involved decimal numeration, where Steinle and Stacey's work (Steinle & Stacey, 2003) on the Decimal Comparison Test provided an example of what is needed: a test that is quick to administer to a whole group, easy for teachers to interpret, and which reveals the underlying conceptual development of students, so highlighting areas for teaching to target. The usefulness of Steinle's approach has been widely acclaimed by teachers. This gave us the prototype smart test, which was central to developing the idea of SMART::tests. The common features of SMART::tests are that they can be administered to a group in a short time, focus on conceptual understanding of key ideas, and can lead to insightful diagnoses at a level of detail that can inform follow-up teaching.
The creation of smart resources embeds advanced research into artefacts that are easy for practitioners to use, creating 'distributed intelligence' in tools. When planning the teaching of a new topic, the SMART::tests and diagnoses provide teachers with better knowledge of the mathematical thinking of their current students. Incidentally, yet importantly, teachers also learn about the mathematical knowledge of students more generally.
We hypothesised that using the recommended smart teaching strategies would provide enhanced instruction
for the current students, and that this would also build teachers' capacity for future teaching.
Testing whether this growth of teachers' Mathematical Pedagogical Content Knowledge (MPCK) actually
occurred was a key research aim; there is now international consensus in the research literature
that teacher quality and especially their discipline-specific teaching expertise is a major determinant
of overall student learning outcomes.
In addition, there were two knowledge transfer outcomes. We intended that teachers' MPCK would improve by
using the resources. However we also intended that the distributed intelligence in the SMART::tests system would
provide expert advice for teachers regardless of whether their MPCK was well advanced, and thereby make
a personalised learning approach easier and more practical for all teachers.
Steinle, V. & Stacey, K. (2003). Grade-Related Trends in the Prevalence
and Persistence of Decimal Misconceptions. In Zilliox JT, Dougherty BJ & Pateman NA (Eds),
Proceedings of the 2003 Joint Meeting of PME and PMENA. 4 259-266. Honolulu, United States:
College of Education, University of Hawai'i.

Publications
| A current list of available research relating to SMART::tests is able to be accessed here.
This list contains abstracts with links to original published versions of research papers. |
| A subset of the full list is below. Authors' copies can be accessed directly through links in the section. |
|
Akhtar, Z. & Steinle, V. (2013) Probing students' numerical misconceptions in school algebra. In V. Steinle, L. Ball & C. Bardini (Eds.) MERGA36-2013 Yesterday, today and tomorrow (Proceedings of 36th annual conference of the Mathematics Education Research Group of Australasia). (pp. 36 - 43) Melbourne, VIC: MERGA. (abstract) |
|
Baratta, W., Price, E., Stacey, K., Steinle, V., Gvozdenko, E. (2010) Percentages: The effect of problem structure, number complexity and calculation format. In L. Sparrow, B. Kissane, C. Hurst (Eds.) MERGA33-2010 Shaping the Future of Mathematics Education. Proceedings of 33rd annual conference of the Mathematics Education Research Group of Australasia . (pp. 61 - 68) Fremantle: MERGA. (abstract) |
Chick, H. (2009). Teaching the Distributive Law: Is Fruit Salad Still on the Menu? In R. Hunter, B. Bicknell, T. Burgess (Eds). Proceedings of the 32nd annual conference of the Mathematics Education Research Group of Australasia. (vol 1, pp. 121 - 128) Wellington: MERGA ( abstract ) |
Chick, H. L., & Baratta, W. (2011). Teachers' strategies for demonstrating fraction and percentage equivalence. In J. Clark, B. Kissane, J. Mousley, T. Spencer, & S. Thornton (Eds.), Curriculum in focus: research guided practice. Proceedings of the 23rd biennial conference of The Australian Association of Mathematics Teachers Inc. and the 34th annual conference of the Mathematics Education Research Group of Australasia Inc . (pp. 183-191). Adelaide: MERGA/AAMT. (abstract) |
|
Price, B., Stacey, K., Steinle, V., Chick, H., Gvozdenko, E. (2009). Getting SMART about Assessment for Learning. In D. Martin, T. Fitzpatrick, R. Hunting, D. Itter, C. Lenard, T. Mills, L. Milne (Eds). Mathematics - Of Prime Importance. Proceedings of the 2009 Annual Conference of the Mathematical Association of Victoria. (pp. 174 – 181) Mathematical Association of Victoria: Melbourne. (abstract) |
|
Price, B., Stacey, K. Steinle, V., Chick, H., Gvozdenko, E. (2011) Getting SMART About Assessment for Learning in 2011. Reflections , 36 (3), 3 - 7. (abstract) |
Price, B., Stacey, K., Steinle, V., Gvozdenko, E. (2013). SMART online assessments for teaching mathematics. Mathematics Teaching (235). (pp. 10-15). (abstract) |
Stacey, K., Price, B., Steinle, V., Chick, H., Gvozdenko, E. (2009). SMART Assessment for Learning. Paper presented at the Conference of the International Society for Design and Development in Education, Cairns,
Australia, September 28 – October 1, 2009. |
Stacey, K., Price, B., Steinle, V (2012) Identifying stages in a learning hierarchy for use in formative assessment - the example of line graphs. In J. Dindyal, Cheng L-P, Ng, S-F (Eds) Mathematics Education: Expanding Horizons Proceedings of the 35th Annual Conference of Mathematics Education Group of Australasia . (pp. 393 - 400). Adelaide: MERGA. (abstract) |
Stacey, K. (2013) Bringing research on students' understanding into the classroom through formative assessment In V. Steinle, L. Ball & C. Bardini (Eds.) MERGA36-2013 Yesterday, today and tomorrow (Proceedings of 36th annual conference of the Mathematics Education Research Group of Australasia). (pp. 13 - 20) Melbourne, VIC: MERGA. (abstract) |
Stacey, K., Steinle, V., Price, B., Gvozdenko, E. (2018) Specific Mathematics Assessments that Reveal Thinking: An Online Tool to Build Teachers’ Diagnostic Competence and Support Teaching. In T. Leuders, K. Philipp, J. Leuders (Eds), Mathematics Teacher Education: Diagnostic Competence of Mathematics Teachers, 11(241-261). Springer. (abstract) |
Steinle, V., Gvozdenko, E., Price, B., Stacey, K., Pierce, R. (2009). Investigating students’ numerical misconceptions in algebra. In R. Hunter, B. Bicknell, T. Burgess (Eds). Proceedings of the 32nd annual conference of the Mathematics Education Research Group of Australasia . (vol 2, pp. 491 - 498) Wellington: MERGA (abstract) |
Steinle, V. & Stacey, K. (2012) Teachers' Views of using an on-line, formative assessment system for Mathematics. Pre-proceedings. 12th International Congress on Mathematical Education Topic Study Group 33 8 July - 15 July, 2012 , (pp 6721 - 6730). COEX, Seoul, Korea. (abstract) |
Abstracts
Abstract of Akhtar, Z. & Steinle, V. (2013)
This study was designed to probe students' thinking about which numerical values can be assigned to algebraic letters. The data from students in Year 7 (n=533), Year 8 (n=377) and Year 9 (n=172) was analysed using response patterns. The data confirmed that eacvh year contained students with two different misconceptions; Different Letter means Different Number and the Empty Box misconceptions. The findings provide support for the Steinle et al (2009) hypothesis that a previously identified response pattern is a subset of the Empty Box misconception.
Abstract of Baratta, W., Price, E., Stacey, K., Steinle, V., Gvozdenko, E. (2010)
This study reports how the difficulty of simple worded percentage problems is affected by
the problem structure and the complexity of the numbers involved. We also investigate
which methods students know. Results from 677 Year 8 and 9 students are reported.
Overall the results indicate that more attention needs to be given to this important topic.
Simple unit fraction equivalents seem to be emphasised, at the expense of fundamental
definition ("out of a hundred") and apparently easy percentages such as 30%. The draft
National Curriculum gives better guidance on the variation amongst percentage problems.
Abstract of Chick, H. (2009)
Introducing algebra in high school is a teaching challenge, where appropriate
explanations and representations are essential. This study examines teachers' reactions
to a page of explanation about the distributive law from a textbook, and investigates
their pedagogical content knowledge about the teaching of algebra. Teachers were
aware that students have difficulties with algebra, but the study shows that some of their
strategies for teaching it are mathematically unsound. In particular, "fruit salad"
approaches are still prevalent.
Abstract of Chick, H. L. (2010)
Ratio (and associated topics such as fractions and proportion) is known to be an area of
mathematics that students find difficult. Multiplicative thinking is necessary, and students
benefit from a wide range of strategies and representations for interpreting ratio. This study
examined aspects of teachers' pedagogical content knowledge for teaching ratio, and
investigated their knowledge of a typical misconception together with the strategies that
they would use for dealing with such a misconception. The nature of the numerical
examples that they suggested might be useful in teaching was also examined. Most teachers
were able to recognise the misconception, but not all were able to generate examples that
might help students to deal with it. Teachers also appeared to have only a limited repertoire
of strategies to assist students.
Abstract of Chick, H. L., & Baratta, W. (2011)
Ratio (and associated topics such as fractions and proportion) is known to be an area of
mathematics that students find difficult. Multiplicative thinking is necessary, and students
benefit from a wide range of strategies and representations for interpreting ratio. This study
examined aspects of teachers' pedagogical content knowledge for teaching ratio, and
investigated their knowledge of a typical misconception together w ith the strategies that
they would use for dealing with such a misconception. The nature of the numerical
examples that they suggested might be useful in teaching was also examined. Most teachers
were able to recognise the misconception, but not all were able to generate examples that
might help students to deal with it. Teachers also appeared to have only a limited repertoire
of strategies to assist students.
Abstract of Price, B., Stacey, K., Steinle, V., Chick, H., Gvozdenko, E. (2009)
"Specific Mathematics Assessments that Reveal Thinking" - or smart
tests - provide teachers with a quick and easy way to conduct assessment
for learning. Using the internet, students in years 7, 8, and 9 undertake a
short test that is focussed strongly on a topic selected by their teacher.
Students' stages of development are diagnosed, and sent to the teacher
within minutes. Many tests have been produced and are now being trialled
in 7 Victorian schools. Where available, on-line teaching resources are
linked to each diagnosis, to guide teachers in moving students to the next
stage. This project is sponsored by the Australian Research Council and
Victoria's Department of Education and Early Childhood Development.
Abstract of Price, B., Stacey, K. Steinle, V., Chick, H., Gvozdenko, E. (2011)
"Specific Mathematics Assessments that Reveal Thinking" - or smart tests - provide teachers
with a quick and easy way to conduct assessment for learning. Using the internet, students in
years 7, 8, and 9 undertake a short test that is focussed strongly on a topic selected by their
teacher.
Students' stages of development are diagnosed, and sent to the teacher within minutes. Many
tests have been produced and are now being used in schools. Where available, on-line
teaching resources are linked to each diagnosis, to guide teachers in moving students to the
next stage. This project was sponsored by the Australian Research Council and Victoria's
Department of Education and Early Childhood Development.
Abstract of Price, B., Stacey, K., Steinle, V., Gvozdenko, E. (2013)
Assessment is 'part and parcel' of mathematics teaching.
Teachers make assessments as they interact with students in many ways and in variety of formats and media.
The best assessment has a diagnostic element within its functionality.
It is important for assessment to be reported upon within the shortest possible timeframe.
Technology can enable sophisticated assessment to be engaged with and reported upon swiftly,
and in the classroom. Here is an example of sophisticated online assessment that is available to all teachers .. now.
Abstract of Price, B., Stacey, K., Steinle, V., Gvozdenko, E. (2014)
This study reports on the use of formative, diagnostic online assessments for the topic percentages. Two new item formats (drag-drop and slider) are described. About one-third of the school students (Years 7 to 9) could, using a slider, estimate “80% more than” a given length, in contrast with over two-thirds who could estimate “90% of” a given length. While four-fifths of the school students could, using drag-drop cards, choose the 2-step calculation of a reduced price after a 35% discount, only one-third could choose the corresponding 1-step calculation.
Abstract of Stacey, K., Price, B., Steinle, V., Chick, H., Gvozdenko, E. (2009)
"Specific Mathematics Assessments that Reveal Thinking," which we
abbreviate to "smart tests," provide teachers with a quick and easy way to
conduct assessment for learning. Using the internet, students in years 7, 8,
and 9 undertake a short test that is focused strongly on a topic selected by
their teacher. Students' stages of development are diagnosed, and sent to
the teacher immediately. Where available, on-line teaching resources are
linked to each diagnosis, to guide teachers in moving students to the next
stage. Many smart tests are now being trialled in schools and their impact
on students' and teachers' learning is being evaluated. Design issues are
discussed.
Abstract of Stacey, K. Price, B., Steinle, V (2012)
This paper discusses issues arising in the design of questions to use in an on-line computerbased formative assessment system,
focusing on how best to identify the stages of a learning
hierarchy for reporting to teachers. Data from several hundred students is used to illustrate
how design decisions have been made for a test on interpreting line graphs.
Abstract of Stacey, K. (2013)
'Specific Mathematics Assessments that Reveal Thinking' (abbreviated as 'smart tests') provide on-line formative assessment of middle years students. They aim to put information from research on students' understanding directly into the hands of teachers, by providing quick automated diagnosis of learning for all students in a class. The Reflections test is used as an example to describe item presentation, evidence identification, and reporting to teachers, and highlight how pedagogical content knowledge can be built.
Abstract of Stacey, K., Steinle, V., Price, B., Gvozdenko, E. (2018)
In this chapter, we describe the design of an online system for the formative assessment of students’ understanding of mathematics and discuss how it develops diagnostic competence and influences teaching. The smart-test system covers many mathematics topics studied by students between about 10 and 16 years of age. It is programmed to provide teachers with an automated diagnosis of their own students’ stages of development in specific topics and to report on an individual’s errors and misconceptions, in order to inform teaching. Our claim is that teachers’ diagnostic competence increases when they have easy access to information about their own students’ thinking. In turn, this can further improve teaching, and hence learning. By drawing together evaluative data from four sources, we highlight aspects of teachers’ initial responses to formative assessment and the effect of using this system on their knowledge for teaching and the subsequent changes to teaching practice. Overall, teachers report that using the smarttests has improved their knowledge of the thinking of individual students as well as of students in general (i.e., their pedagogical content knowledge), and that they can use this information in several ways to adjust their teaching. Paradoxically, using smarttests reduces the demand for teachers to have specific knowledge for diagnosis and at the same time increases this knowledge and so improves their diagnostic competence.
Abstract of Steinle, V., Gvozdenko, E., Price, B., Stacey, K., Pierce, R. (2009)
Details are provided of simple algebraic items which can be used to detect two
particular ways students think about the numerical meanings of letters (in contrast to
non-numerical thinking). The data from Year 7 students (n=228) and Year 8 students
(n=139) on these items is analysed using response patterns to probe student thinking.
Less than 10% of the students were correct on these items whilst the prevalence of the
two most common error patterns is 20%-30% at each year level. New response patterns
are detected, indicating that further improvements to the items will enable students'
thinking to be investigated further.
Abstract of Steinle, V. & Stacey, K. (2012)
In this paper we discuss some issues arising from teachers' use of an on-line system for
formative assessment of their students' understanding of mathematics. The 'smart tests' cover
many topics in secondary school mathematics, and are programmed to provide an automated
diagnosis of students' stages of learning in specific topics, to inform teaching. In particular,
we highlight teachers' views about: the desirability of formative assessment; the use that they
make of this information; the provision of feedback; and the effect of using the system on
their pedagogical content knowledge and subsequent changes to their practice .Overall,
teachers report that use of the tests improves their knowledge of the achievement of
individual students and students in general, and that they can use this information in several
ways to improve their teaching.